A Predator Prey Model With Evolution in Agents.jl

Using Julia's Agents.jl to model predator-prey populations adapting to each other

Jan 09, 2024

I’ve always been fascinated with the dynamics of evolution. It is incredible to me how predators and prey evolve together in order to sustain themselves. Unfortunately, coming by experimental data of real-time evolution is difficult, so we must resort to some kind of artificial simulations.

To do so, one might recall predator-prey models from their introductory differential equations class. Despite being toy examples, they are a perfect example of how real world phenomena can be distilled to very simple concepts and still provide a lot of insight when modeled properly.

Even though simple models have been proven to answer a lot of questions, they can’t do everything. To answer harder questions that require more variables—such as ones involving adaptations to other organisms—we need to expand our models. To work from the ground up, we will start off with the most basic predator prey model and work our way up to a model that can give us insight into a population of organisms adapting to each other over time.

In the end, I summarize the findings and emphasize some unexpected discoveries in the way our model evolves—make sure to read conclusion for my analysis of the results.

Introduction to the Lotka-Volterra Equations

The classic Lotka-Volterra equations are a wonderful way to represent interaction between predator prey populations:

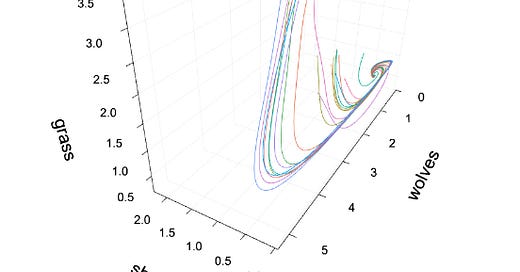
\(\frac{dx}{dt} = x(\alpha - \beta y), \quad \frac{dy}{dt} = y(\gamma x - \delta)\)

The familiar equations describe the growth rate of a population of sheep—the prey—and wolves—the predators. It is clear from the equations that the assumptions the model makes is that more prey, or a higher `x`, increases the growth rate of both the prey and the predators, while more predators, a higher `y`, decreases the growth rate of the prey and can decrease the growth rate of the predators. Here is an example of the solution to the ODEs:

Solutions to the Lotka-Volterra equations for 10 different initial values. The solutions form periodic orbits that are approximately centered around 1.2 prey and 0.5 predators. As you move further away from the center, the orbits become less circular and begin to resemble an equillateral right triangle that makes a 90 degree angle with the x and y axes. — Source: By Brice2000 - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=44187098

Each dot represents a different initial starting value for the number of predators and prey, and the orbits represent how the populations change over time according to the ODEs.

While the assumptions may be simplistic, the resulting dynamics (which you can dive into on the Wikipedia page) can actually be found in some ecosystems and even economic models.

An Example of a Simple Extension to the Lotka-Volterra Equations

Still, we can further extend the Lotka-Volterra equations to understand more complicated dynamics such as introducing grass, represented by `z`, which would interact with the sheep population as such (the predator ODE would remain unchanged):

\(\frac{dz}{dt} = z[\epsilon (\zeta - z) - \eta x], \quad \frac{dx}{dt} = x[\alpha(z-\theta x) - \beta y]\)

This time, I will leave it up to you to figure out what assumptions I made and what the constants mean (hint: it would be quite unnatural for the grass to grow to infinity in the absence of any sheep, there must be a limit; and sheep should only grow if there is sufficient food to sustain the population). If you disagree, by all means, share your ideas in the comments!

This system of ODEs, too, should yield some interesting dynamics. Using Julia, we can solve the ODEs using a simple Euler solver and obtain the following plot:

20 multicolored lines starting at random positions in two seperate clusters at the top left of the 3d plot sweep down in the -z, +y, and -x direction; make a sharp backwards turn in the -y direction; and converge to an attractor at approximately .3 sheep, .3 wolf, and 1.0 grass — Each line represent the trajectory of a different initial value according to the modified Lotka-Volterra equations that we set up. In this particular plot, the parameters used all had a value of 1.

For my choice of parameters (all 1’s), it looks like there is an attractive point where all the plotted initial values converge to. If you are able to, I encourage you to run the code for yourself, explore other initial values and parameters, or even test out different forms of the ODEs.

Exploring More Complicated Interactions With Agent Based Modelling

But what if we wanted to explore situations that demand more than the modelling of simple population dynamics? For example, what if we could prescribe a certain poisonous gene to the sheep that wolves can develop a genetic resistance to and see how the genetic pools evolve over time. To be more specific, imagine a sheep-wolf-grass environment that obeys the following rules:

We have a 30 by 30 grid of grass that can be eaten by sheep, and each patch takes 30 days to fully grow after being eaten.
Our sheep are poisonous, and the type of poison the sheep secretes is determined by a gene represented by a number between 0 and 1.
- The sheep’s number from 0 to 1 will be referred to as a ‘gene number’
Each wolf is naturally immune to a certain range of toxins. The center of that range is determined by another gene that ranges from 0 to 1 and is found in each wolf.
- The wolves’ number from 0 to 1 will be referred to as a ‘gene center’ and their range will be referred to as the ‘gene_range’
When wolves and sheep reproduce, their offspring is a perfect clone of themselves except the offspring’s gene number is given a random mutation.
- The gene center, however, will remain constant

A 30 by 30 grid of green squares representing fully grown grass and brownish-green squares representing growing grass (the more green it is the more grown it is). There are many grey triangles representing wolves and a few white circles representing sheep at random points on the grid. — A visualization of our environment. The triangles are wolves and the circles are sheep. Green squares are fully grown grass and the brown patches are grass that are still growing. Source: Predator-Prey dynamics example on Agents.jl docs, https://juliadynamics.github.io/Agents.jl/stable/examples/predator_prey/

With such an environment, it could be interesting to see how the gene distributions run away or chase each other, how mutation and reproduction rates can affect stability, and which populations are are to sustain themselves.

If we want to answer these questions, we need some way to simulate them. However, I certainly cannot think of a system of differential equations which can capture these rules, but—luckily—I don’t have to. Using Julia and Agents.jl, we can employ agent based modelling to actually simulate a population of sheep, wolves, and grass with these rules hard-coded into their behavior.

Due to the popularity of predator-prey models, the Agents.jl package already published an example of discrete predator-prey population dynamics with sheep, wolf, and grass populations. Our job will then be to add in our gene functionality which includes giving wolf and sheep a gene, some way to mutate the gene when reproducing, and only allowing the wolves to eat sheep when they fall within their gene range.

In the next subsection, I will be giving a quick look into how the simulation works and explaining some of the Julia code. Any reader should safely be able to skip the upcoming section if they don’t want to read code or just want to see how such a system evolves over time.

Assigning Genes and Mutation Rates to Agents and Grass

All code can be found in this GitHub repository.

Assigning genes, gene ranges, and mutation rates to the agents (the sheep and the wolves) is as easy as adding new fields to the Sheep and Wolf structs.

@agent Sheep GridAgent{2} begin
    energy::Float64 # If energy falls below 0, the Sheep dies
    reproduction_prob::Float64 # Chance of reproducing after each step
    Δenergy::Float64 # Energy gained from eating Grass
    gene::Float64 # Gene number from 0 to 1
    mutation_rate::Float64 # Mutation rate
end

@agent Wolf GridAgent{2} begin
    energy::Float64 # If energy falls below 0, the Wolf dies
    reproduction_prob::Float64 # Chance of reproduction after each step
    Δenergy::Float64 # Energy gained from eating Sheep
    gene_center::Float64 # The gene number between 0 and 1 for Wolves
    
    # Each Wolf can only eat if |Sheep.gene-Wolf.gene_center| < Wolf.gene_rage
    gene_range::Float64
    mutation_rate::Float64 # Mutation rate
    hunt_range::Int # Vision range for finding edible Sheep
end

The mutation_rate fields come into play when a new agent is added or when grass spreads. For example, in the following code block that is run every time a sheep reproduces, the cloned sheep copies all the traits of the original sheep except its gene number is the original sheep’s gene number plus a random variable randomly sampled from a normal distribution of mean 0 and standard deviation of mutation_rate

function reproduce!(agent::Sheep, model)
    # Halves the energy of the sheep that is reproducing
    agent.energy /= 2

    # Creates a new sheep with a gene number of whatever the current sheep's     
    # gene number is plus a random number drawn from a normal
    # distribution of mean 0 and std of mutation_rate.
    # Every other field is a perfect copy of the current sheep
    id = nextid(model)
    mutated_gene = clamp(agent.gene + rand(model.rng, Normal(0, agent.mutation_rate)), -1, 1)
    offspring = Sheep(id, agent.pos, agent.energy, agent.reproduction_prob, agent.Δenergy, mutated_gene, agent.mutation_rate, agent.hunt_range)
    add_agent_pos!(offspring, model)

    return
end

Results of the Simulations

Sheep and Wolves

Now that we have everything set up, we can begin to ask questions about how the genes evolve over time. Let’s see how the populations and gene distributions of wolves and sheep change over time by graphing histograms of their genes over time (the grass is excluded since it doesn’t have any poisonous genes, but know that it’s population oscillates opposite to that of the sheep).

A plot of a blue histogram with a red histogram overlayed. The blue histogram represents the sheep and we can see it oscillating beteen peaking at -1 and tapering off to 0 at 1 and peaking at 1 and tapering off at -1. The red histogram is much smalle in comparison and it seems to be chasing the blue peaks from side to side, wherever the red histogram is, the blue histogram is on the other side. — The gene distributions of sheep and wolves in blue and red, respectively. Notice how the wolves’ distribution is chasing that of the sheep. The effect is also quite periodic.

As someone familiar with the concept of evolution would expect, the wolves’ histogram is seen to be ‘chasing’ the sheep’s histogram. This translates into the gene pool of the wolves moving closer to that of the sheep and the sheep’s gene pool moving further away from that of the wolves. Of course, this is explained by the wolves eating an sheep within its gene pool and leaving the ones outside to reproduce in relative safety.

We can visualize chase by graphing the mean gene values for both sheep and wolves over time. By doing so, we also notice that it their ‘seasons’ are quite periodic.

A graph with the x axis from 0 to 2000 time-steps and y axis from -1 to 1. The blue line describes the sheep's gene distribution and has a blue shaded ribbon around it that depicts the standard deviation at that point. The red line, similarly, depicts the wolves' gene means and standard deviations. As the blue line oscillates approximately sinusoidally, the red line makes triangular waves to try and match the blue line. The standard deviation is seen to peak at the peaks and valleys of both lines while thinning in the transition periods. — The mean gene values for sheep in blue and the mean gene values for wolves in red. The ribbons around the line depict the standard deviation of the distributions. Plotted for 2000 time steps.

If we increase the wolves’ mutation rate, the red line is able to keep up very well with the sheep’s distribution:

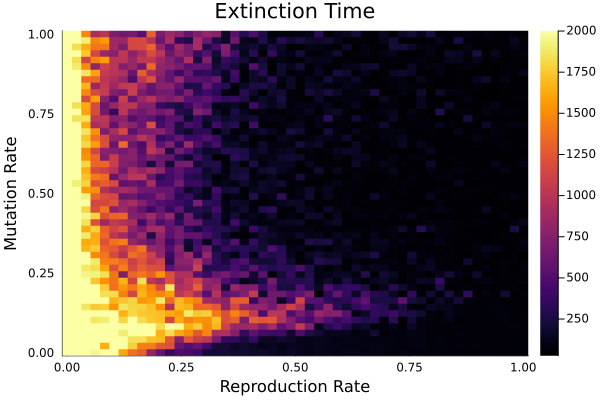
However, the only reason the sheep are able to stay alive is because I set the wolves’ reproduction rate and range of immunity to be very low. Increasing either one quickly killed off all the sheep. If we want to entertain higher wolf reproduction rate or immunity ranges, a lower mutation rate was needed. The following heat map of wolf extinction times might interest some readers:

Heat map of wolf mutation rate vs reproduction rate. The heat values proportional to the timesteps that the wolves survived for with 2000 being the maximum and 0 the minimum. We see that the map is hot on the left edge for any x value under ~0.6 and rapidly cools to 0 timesteps around ~.4 reproduction rate. However, there is one spike that juts out from the left with a narrow peak around ~0.15 mutation rate. The spike cools to 0 timesteps around ~0.75 reproduction rate. — Heat map of mutation rate of the wolves vs the reproduction rate. The heat values are determined by how long the wolves were able to survive in that simulation. This was done when the sheep reproduction and mutation rates were both 0.3. I would love to see how this plot changes as the sheep’s parameters change, but I do not have the computational resources to do that (this alone took 4 hours!)

Sheep and Grass

I left out the grass since they didn’t have any poisonous genes, but what if they did? What if sheep could only eat grass that secretes poison that is similar in gene number to its own poison?

As we did with the sheep and wolf populations, lets first take a look at how their gene distributions change over time:

A green and blue, for grass and sheep, respectively, histogram animation. The histograms initially start on the left edge of the graph at -1 and decay down as they reach the right side of the graph at +1. As the animation progresses, both histograms even out to become roughly uniform between -1 and +1 and continue to only have slight pertrubtations away from uniform distributions. — Evolution of a population of sheep and grass when both initially start out with a gene distribution sampled from a normal distribution of mean -1 and std 0.3 (truncated to be between -1 and 1). This pattern of evening out and having uniform gene distributions was observed in nearly all combination of sheep and grass parameters.

Surprisingly, they start at their specified initial distributions and then even out over time. Even though such a scenario was never observed with just sheep and wolves, for sheep and grass, this pattern was present for nearly all combinations of initial distributions, reproduction rates, and mutation rates (there were some very rare situations where the sheep died out—try to see if you can make up a scenario which forces the extinction of sheep).

Sheep, Wolves, and Grass

Now, what if we take the next step and try to introduce the wolves into this sheep-grass system? Well, my first 100 attempts at finding a stable system looked like this:

A green, white, and black line representing grass, sheep, and wolf populations, respectively. In intervals of about 50 timesteps, the grass population starts off at 450 and spikes to about 500, then it dips to 100, and rises all the way to 900. The sheep start at 80, dip a little, rise to 300, and fall to 0. The wolves start at 10, rise exponentially to 200 by timestep 100, and then die off after the sheep do. — Wolves overpowering the sheep and only leaving an empty grid of grass.

Trying to find what kinds of wolf populations could be sustained by the environment was no easy task. If we don’t consider the initial population numbers, initial distributions, energy gained from eating, and and hunting ranges, there are a total of 7 variables—all numbers between 0 and 1—that we can control (I will say which variables in a moment, their specifics are not too important right now). That means we would need to search in a seven dimensional grid for stable conditions. With just two organisms exhibiting poisonous adaptations (sheep and grass or sheep and wolves), we were lucky enough to find that nearly any initial configuration was stable, but finding the right conditions for the wolf population be able to sustain itself was much more difficult.

In most cases, the wolves would quickly rise in numbers no matter how small the initial population was, eat all the sheep, and then starve themselves to death—leaving only a lush 900 patches of grass. Another common scenario was that the wolves nearly deplete all the sheep, lose most of their population due to the low sheep population, and then not reproduce fast enough to replace themselves before they die of exhaustion (if a wolf’s energy level dips below 0 it dies, and it takes 1 energy to move). The sheep, however, pull through and they happily live on eating grass for the rest of the simulation.

Green, grey, and black lines repesent grass, sheep, and wolves, respectivel. In the beginning, all the lines zigzag up and down the graph and wildly shift population numbers from 0 to 750. But at around timestep 300, wolves suddely die out and the sheep and grass populations slowly stabilize after 200 timesteps to oscillate around 300 and 150, respectively — Sheep living happily for the rest of the simulation after the wolves die out around 300 time steps.

Brute forcing through the 7-dimensional state space to find stable configurations would take forever, which is why I wrote a simple Particle Swarm Optimization (PSO) algorithm to find the combination of variables for which the wolf population is able to stay alive for the longest. I will not be going into how the PSO algorithm works here, but curious readers can reference sections 16.1.1-16.1.5 of these notes for a good geometric intuition or the Wikipedia page for some fast facts. For our purposes, you just need to understand that some n particles collectively search and adjust their trajectory towards the best positions in the 7 dimensional space.

During the optimization process, we also generate some data to play around with—in our specific implementation, we had 20 particles in the swarm and each particle made 100 searches, so 2000 data-points in total. This means the PSO can be useful in two ways: finding a good set of parameters for a stable wolf population and allowing us to explore, in a very loose sense, the regions of our seven dimensional space which are most likely to produce stable populations. The latter was of particular interest to me since I wanted to know what sets stable configurations apart.

Running the PSO, we can plot out various 2d relationships in a pairwise plot to see if we can find any regions of stability. In the following plot, redder regions correspond to those positions that the PSO algorithm preferred to find stable configurations in. If we allow all parameters to range between 0.1 and 1 (while technically values of 0 are allowed, configurations where, say, wolf populations that just don’t grow at all over time won’t be very interesting; and, indeed, when I do allow PSO to pick values of 0, it sets as many variables to 0 as soon as possible), the regions PSO explored can be plotted as follows (and for the long-awaited reveal of the 7 variables):

Pairwise plot of 7 variables: sheep reproduction rate, wolf reproduction rate, sheep mutation rate, wolf mutation rate, grass mutation rate, grass gene range, and wolf gene range. The red regions are the regions where the PSO algorithm found the most stable configurations. The values for all seven variables could range from 0 to 1, but the PSO was restricted to searching between 0.1 to 1.

Hey, I never said it would look pretty. When looking at this pairwise plot, you should keep in mind that the red regions do not exactly correspond to the regions where stable configurations are the most likely (I defined a stable configuration as one where to wolves survive for at least 2000 time-steps). Instead there is a subtle difference: the red regions is where the PSO algorithm most preferred to look for stable solutions. We can distill the findings from the pairwise plot into a few observations about the PSO’s preferences.

The PSO algorithm preferred looking in regions where

sheep_reproduce has a value less than 0.3
wolf_reproduce, wolf_mutation_rate, grass_gene_range, and wolf_gene_range are all extremely low—all very near to 0.1 by the looks of it.
sheep_mutation_rate was above 0.5. But this variable had some more freedom since we can see a few times when stable configurations were found at lower values.

As for two dimensional relationships, we also have

lower sheep_mutation_rate rates correspond with slightly lower sheep_reproduce values
as grass_mutation_rates decrease, the PSO algorithm converges to a sheep_reproduce value of ~0.15.

To point out just how delicate this system is. When I change the minimum value of the variables to be 0.2 rather than 0.1, the PSO algorithm is completely lost. The best run it had only sustained wolves for about 450 time-steps and the pairwise plot (literally) pales in comparison. The few iterations that produced stable outputs in the above pairwise plot were all very uneventful as seen in the following animation

A green, red, and blue, for grass, wolves, and sheep, respectively, histogram animation. The blue and green histograms initially start on the left edge of the graph at -1 and decay down as they reach the right side of the graph at +1. As the animation progresses, both histograms even out to become roughly uniform between -1 and +1 and continue to only have slight pertrubtations away from uniform distributions. The red histogram forms a clump in the center which is at 0 and remains there for the whole simulation. — The very uneventful simulation of all three living things: sheep, wolves, and grass. The sheep and grass exhibited the same evening behavior that we observed in isolation, but the wolves seem to hardly have an effect on the sheep and hardly change in population size.

We see that the grass-sheep interaction dominates the evolution as they even out in gene distributions, but the wolf population hardly interacts with the sheep. The only stable configurations that PSO found seem to all diminish the effects of the wolves. Clearly, in our environment, a three body system of genes is very unsustainable. Gene interactions had to be limited to being between only two organisms at a time in order for a stable ecosystem.

Concluding Thoughts and Summary

As I hoped, modelling poisonous organisms allowed to me to view evolutionary mechanisms that push predator-prey pairs to continually try and eat and evade one another, respectively. It was interesting to find that the model did not present any equilibrium states where both the sheep and wolf gene distributions stayed constant, I wonder if organisms in nature are also continuously evolving instead of finding equilibrium. It’s hard for me to tell because I’m no biologist and also I’ve never observed evolution in real time, so I sadly have don’t have an intuitive grasp on how it works.
As to why the wolves’ distribution can be seen to chase that of the sheep, but the grass’ distribution evens out over time if given a poison trait, I have no good explanation! If someone can provide a testable idea for me to try out, I would love to fill in this gap with a working theory.
Even though I could not find stable three organism dynamics, something interesting to note about this whole experiment is that the basis of the ‘genes’ was some kind of poison secretion/adaptation; while there are plenty of examples of organisms developing resistance to toxins in order to access a food source, I cannot seem to find any examples of three different organisms in different trophic levels whose poisonous adaptations all interact with one another like in the sheep-wolf-grass system (for example, I want to find something like a poisonous frog being eaten by immune predators, and, at the same time, eating insects that give off the same poison).

I am certain that assuming the rarity of three organism with the same type of poison adaptations is explained by this model is a gigantic leap in logic. I openly admit that I have no evidence of any physical relevance of this model! However, even if nothing is true, it was still an interesting exercise in agent based modelling, predator-prey dynamics, visualizations, and also playing around with the parameters taught me about some of the the complex interactions that ecosystems exhibit—not nearly as intuitive as the functions I am used to dealing with as a physics and mathematics student!

Some next steps that I (or maybe a motivated reader who I would be very happy to respond to if they reached out) might try to implement are:

Pack/herding behavior for the wolves and sheep to find more optimal ways to hunt prey/evade predators
More complex boundaries such as narrow passage ways and mountains to observe genetic drift due to geographic isolation
Have more than one gene (such as poison as well as camouflage) which I conjecture should allow for more than two organisms’ genes to interact at once
External factors such as viruses or weather

This is my first post on Substack, and I hope to keep this updated with more projects (and maybe puzzles) in physics, mathematics, and computational sciences. If you enjoyed what you read or have feedback, let me know!

Hasith’s Substack

Discussion about this post